
Среди различных видов колебаний наиболее простой формой является гармоническое колебание, то есть такое, при котором колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса.
x = Аcos(wоt + jo),
где wоt + jo = j - фаза колебаний; jo - начальная фаза (при t=0); wо - круговая частота колебаний, А - их амплитуда.
Амплитуда и начальная фаза колебаний определяются начальными условиями движения, то есть положением и скоростью материальной точки в момент t=0. Величина wо определяет частоту колебаний f=wо/(2p) системы.
Гармонические колебания можно изображать с помощью векторных диаграмм. Этот метод состоит в следующем. От начала оси абсцисс проводится вектор А, проекция которого на ось 0X равна Асоsj.
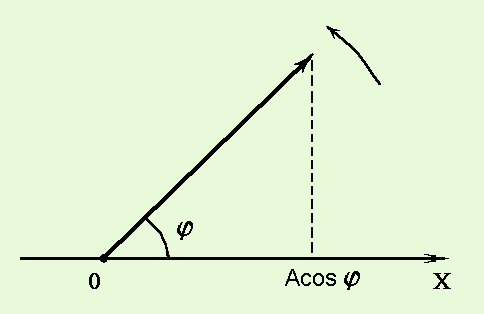
Если вектор А равномерно вращается с угловой скоростью w о против часовой стрелки, то wоt + jo = j , где jo - начальное значение j, и проекция вектора А на ось OX изменяется со временем по гармоническому закону.
В таком представлении амплитуда колебаний есть модуль равномерно вращающегося вектора А, фаза колебаний - угол между вектором А и осью OX, начальная фаза - начальный угол, круговая частота колебаний - угловая скорость вращения вектора А, смещение колеблющейся точки - проекция вектора А на ось OX.
Чтобы найти скорость материальной точки при гармоническом колебании, нужно взять производную от выражения x = Аcos(wоt+jo) по времени:
u = dx/dt = - Awоsin(wot + jo) = umaxsin(wot + jo),
где umax = Awo - максимальная скорость (амплитуда скорости).
После преобразования выражение примет следующий вид:
u = umaxcos[(p /2)+(wot+jo)].
Сравнивая это выражение с гармоническим законом, можно заметить, что фаза скорости на p /2 больше фазы смещения, то есть скорость опережает по фазе смещение на p /2. Продифференцировав выражение u = umaxsin(wot + jo), можно найти ускорение:
a = du /dt = -Awo2cos(wot + jo) = -amaxcos(wot + jo),
где amax=Awo - максимальное ускорение (амплитуда ускорения). Подругому можно записать:
a=amaxcos[p +(wot+jo)].
Из сравнения этого выражения с гармоническим законом следует, что фазы ускорения и смещения различаются на p ,то есть эти величины изменяются в противофазе.

Графические зависимости смещения, скорости и ускорения от времени.

Векторные диаграммы зависимости смещения, скорости и ускорения от времени.
Кинетическая и потенциальная энергии колебательного движения.
Кинетическая энергия колеблющейся материальной точки:
Ек = 1/2mumax2sin2(wot+jo) = 1/2mA2wo2sin2(wot+jo) = 1/2k A2sin2(wot+jo).
Потенциальную энергию можно найти, используя гармонический закон и выражение ЕП = 1/2k x2:
ЕП = 1/2k А2cos2(wot+jo).
Отсюда полная механическая энергия колеблющейся материальной точки:
Е = ЕК + ЕП = 1/2k А2sin2(wot+jo)+ 1/2k А2cos2(wot+jo) = 1/2k А2[sin2(wot+jo) + cos2(wot+jo)]= 1/2k А2.